Mortgage

How mortgage repayments ( amortization ) works:

The math behind remortgage payments is simple, though few people give you it! It's worth looking at to decide how long to take your mortgage over so you can see how a shorter mortgage effects your short-term interest repayment.

Lets take an example mortgage of £250,000 and an interest rate of 3% over 25 years (300) initially and see what happens. The mortgage becomes the Loan Balance at the start of the mortgage (LB0), and the interest rate (APR) is i.

The interest rate for mortgages is charged as an Annual Percentage Rate (APR). Thus over the course of 12 months in the example we pay 3%. However, it's not as straightforward as saying that in the first year therefore we pay (250,000 * 0.03 =) £7,500 in interest as the interest payments are worked out on a monthly basis as 1/12 of the APR of the remaining loan balance (LBn).

So the interest payment for any given month is easy to work out based on the current Loan Balance.

In order to work out the monthly payment we need to use the following equation:

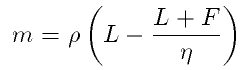
Where:

• m is our monthly payment
• p is the interest rate paid per payment
• L is the principle loan value
• F is the future value (this will always be zero at the end of a mortgage, so use 0!)
• η is the value 1 - ((1 + p)^300) where 300 is the number of month

Expanding to fit our values we get this to plumb in to our calculator: m = 0.0025 * ( 250,000 - (250,000/(1 - ((1 + 0.0025)^300))))

m becomes £1185 as our monthly payment. Hence our first interest payment is 250,000 * (0.03 / 12) = £625 and the amount paid off of the Loan Balance is 1185 - 625 = £560. So we start by paying more interest than balance.

As the monthly amount we pay stays the same the interest we pay (as an amount, not as a percentage!) decreases and hence the more of the Loan Balance we pay off. So the second interest payment becomes: (250,000 - 560) * (0.03 / 12) = £623.60 and the amount paid of the Loan Balance is 1185 - 623.60 = £561.40.

For more information on the maths behind amortization, look at the University of Utah's website

Having proved the maths we can move onto someone else's calculator to do the hard work for us and plumb in the parameters to see how the mortgage repayment is affected. The first thing to do is to make sure the site's calculator agrees with our own calculation.

Go to the Loan Amortization calculator on easycalulation.com and fill in the values we've used as an example here (Leave the month and year as January of this year) and press calculate. Scroll down to the results and you'll see the monthly payment is £1185.53 with the first payment being made up of £625 of interest and £560.53 paid off of the Loan Balance. This proves the sites maths is correct, as is ours.

Now lets look at how the amount of interest we pay is affected by the length of our loan.

Let's fast forward 10 years. Scroll down to January in ten years from the start. We get the following Loan Balance payment and interest payment along with the total left outstanding:

Now change the values in the calculator to take the mortgage out over 15 years instead and look at where we are in 10 years again:

The values have changed pretty significantly. Importantly the monthly payment has changed from £1185.53 to £1726.45, and very interestingly the amount left on the loan remarkably £76,319.64 less.

We've been paying more in, in-fact we've been paying £540.92 extra per month in over ten years. That's £64,910.40 extra we've paid, but we're £76,319.63 further into the loan so after 10 years we've saved £11,409.23 (of course assuming the rate has not changed)

Note the total interest paid over the lifetime of the loan:

£250,000 @ 3% over 25 years: £105659

£250,000 @ 3% over 15 years: £60761

That's a saving of £44,898 over the course of the mortgage. But you've got to stomach the higher monthly payments. Rates vary and they inevitably will go higher at some point (Currently in the UK there's little room for them to move other than up when the economy gets going again) so a buffer zone is required, although you want to pay off as much as possible as quickly as possible. The longer your loan term, the more interest you pay.

Interest Only Mortgages¶

So whilst looking at mortgage options, we also have the interest-only mortgage. It gives you a low interest rate and is designed to allow you to put your Loan Balance payments to work in a seperate savings account. The selling feature is that the interested earned through the savings will make you better off in the long run.

The interest per payment is always on the outstanding Loan Balance as before, but with the caveat that you do not pay anything off of the Loan Balance each month. The money you put into a separate savings account is entirely seperate to the mortgage. This has repercutions. You cannot directly relate savings percentages (APR) to mortgage percentages here.

The Loan Balance is only altered after a certain amount of time and the money in the savings account is placed into the mortgage to reduce the Loan Balance. At this point your interest only payment (essentially your monthly mortgage payment) is reduced because the Loan Balance has decreased and you are now paying a monthly interest payment on a smaller outstanding balance.

Lets look a bit closer:

On a mortgage of £150,000 @ 2.75% APR over 15 years the monthly payment at the start of the mortgage is (150,000 * (0.0275 / 12)) = £343.75. This is a pure interest payment.

If we do the maths for a standard mortgage using the calculator over at easycalculation.com we see that the first interest payment is indeed £343.75 and the first prinicple payment (off the Loan Balance) is £674.18. So we need to be saving £674.18 a month to be on-par with the standard mortgage payment.

The term before the Loan Balance is reduced in an interest only mortgage is decided upon when the mortgage is agreed, but 3-4 years appears to be about the norm.

So lets look in 4 years time:

1. For the standard mortgage, the following interest payments have been made:

2. 343.75, 342.2, 340.66, 339.1, 337.55, 335.99, 334.43, 332.86, 331.29, 329.72, 328.14, 326.56, 324.97, 323.39, 321.79, 320.2, 318.6, 317, 315.39, 313.78, 312.17, 310.55, 308.93, 307.3, 305.68, 304.04, 302.41, 300.77, 299.12, 297.48, 295.83, 294.17, 292.51, 290.85, 289.18, 287.51, 285.84, 284.16, 282.48, 280.8, 279.11, 277.41, 275.72, 274.02, 272.31, 270.6, 268.89, 267.17

...which is a total interest payment of £14,694.38 over the four years. We've paid off £34,166.37 which gives us a new Loan Balance of £115,833.63 at the end of the four year period.

1. For the interest-only mortgage we've been paying the 1/12 of 2.75% of the Loan Balance (LB0) for the entire period (12 * 4 = 48 months) which is a total of £16,500.00 over the four year period.

Assuming that we settle on the same monthly outgoings for mortgage, we've been saving £674.18 per month into our savings account which has totalled (before interest!) £32,360.64.

Working out the interest earned is going to be based on a monthly-interest account figuring a 4.5% interest rate (APR). So each month we earn (4.5/12)% of our current Savings Balance.

In a 4.5% interest (APR) account our savings have reached £35,383.55 which means we have earnt a total of £3022.91 interest.

Paying this off of our Loan Balance means at the end of this period with the interest only mortgage our new Loan Balance to probably re-mortgage again is £114,616.45

That's good, it's £1217.18 better than through a standard mortgage. However, over the course of four years, we've paid an extra (16500 - 14694.38) £1805.62 in interest. So in effect we're £588.44 worse off.

To conclude on interest-only though, you have a life-buffer which is your mortgage savings. You'll have to ensure that a long term high interest account is available - and I've not allowed for taxed savings (All my savings would be skimmed of 40% by our nice government!). Saving this amount of money is well outside your ISA quota, so don't expect ISA's to cover your saving requirements.

Infact, by paying tax on the savings we get a different story:

In a 4.5% interest (APR) account with 40% tax on savings our account has reached £34,132.27 which means we have earnt a total of (34132.77 - 32360.64) = £1772.13 interest.

Paying that off the loan balance results in a balance of £115,867.73 after the four year period. That's (115,867.73 - 115,833.63) = £34.1 worse off on the balance, plus we've paid an extra £1805.62 in interest don't forget. So now it doesn't seem great.

If you only get three percent on your interest (still subbing 40% for tax) our savings only reach £33,528.04 which is only £1167.4 interest. The resulting Loan Balance is £116,471.96 which is £638.33 worse off on the balance and the extra interest paid on the Loan Balance.

The key to interest free is early pay-off. That is we decide early on that we can afford more than the bank will let us have. So we take the same £150,000 mortgage and decide that instead of a monthly payment of £1017.93 each month, we can actually afford £1300 per month instead.

This results in a monthly savings payment of £956.25. Plumbing this into the savings math (and still allowing for 40% tax) we end up with a total of £47,555.82 in the savings account. We've accumulated interest of (£47,555.82 - £45,900) = £1655.82 which pretty much gets rid of the £1805.62 extra interest paid because of the interest being on the starting loan balance every month with this mortgage type.

We now have a large difference however our Loan Balance going forward (i.e. to remortgage). The Loan Balance for the increased payments over four years is ( £150,000 - £47,555.82 ) = £102,444.18. This is a difference of ( £115,833.63 - £102,444.18 ) = £13,389.45! This has cost us (1300 - 1017.93) * 48 = £13,539.36

Of course, you can do this with a standard mortgage payment too. Usually you can over-pay into a normal mortgage which is good because the payment immediately reduces the Loan Balance, but most mortgage providers

Although this looks like there is no gain, that's wrong. The gain is having a lot of transiently available savings. You'll have large sums of money you can pull on if necessary. Of course ultimately this will lengthen your mortgage repayment, but the flexibility means you can live with a lot less stress than having a high montly payment commitment.

Conclusion¶

So what are the compromises associated with these different ways of mortgaging?

Well, simply getting a short-term mortgage means you have to aggressively pay the Loan Balance off and you're trying to minimise the interest you pay. However the effects of the reduced interest are only really seen later on (10yr+) in the mortgage and you must stomach high payments as seen earlier.

A longer term mortgage means you'll be paying more in interest payments (but again the positive effect of this is only seen in the latter stages of the mortgage). You'll have moderately high payments to pay and could save alongside the mortgage up to the montly amount you've set aside for the mortgage. This will give you a small buffer should things go a bit Pete Tong. Some of these mortgages will let you over-pay, but that will mean you are effectively living life with no buffer because you've put it into the Loan Balance of the mortgage. You cannot get access to that money once it's been paid, and you'll also likely get an over-payment charge as the mortgage company like to have the regular interest payments.

Fixed interest works out about even if you can get a decent savings account (even on taxed savings). Some savings can of-course be put into tax-free savings too, any that are investment-based and free from capital gains tax too. You can then be aggressive with your savings because the actual payment required on a monthly basis is the origianl Loan Balance interest payment which is a low figure. The rest of what you decide is a survivable mortgage outlay can be pumped into the savings account. This means there is a lot of money in easy-access savings accounts.

Fixed or variable rate just depends on what the interest rates are going to do and so do not really need to go towards your mortgage type decision.